Control of a Batch
Process |
1) Signals, Systems and Control Department
Faculty of Mathematical Sciences
University of Twente
The Netherlands
2) Kodak Corporation
| To download the application in .pdf format, click here. |
Introduction
However, there frequently are more outputs than ”control knobs” to use for adjustment, and the inputs frequently affect many outputs simultaneously. Testing delay, more outputs than inputs, the desire for a first-order return rather than a step return to target for some products, and stochastic disturbances make this an interesting control problem.
Below is the transfer function plus disturbance model for a process like the one described above.
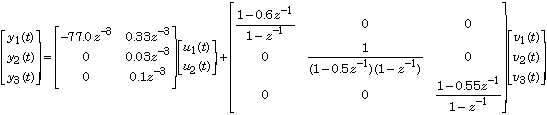
Here
is the delay operator and the 
are disturbance
signals.
The three outputs
, 
and 
successively are the deviations from aim of photographic speed, contrast, and
upper density point. The two inputs 
and 
are dye and laydown changes from preset starting values, and the
delay of three accounts for the zero order hold and testing delay.
The three disturbance models are first order integrated moving average, first order integrated autoregressive, and first order integrated moving average, respectively.
Design TargetsThe control law H for this problem follows by the minimization of a mean square error criterion of the form
E denotes the expectation, e(t) is the deviation of the output y(t) from its set point, and
is the incremental control
action. 
and 
are weighting
matrices.
Fig. 1. Internal Model Control
Process
& Disturbance Models
The control is computed by a polynomial algorithm. To this
end, the plant-disturbance model is rendered as
with D(t) the effect of the disturbances on the output y. The process model
is described by the right polynomial matrix fraction
with L and R polynomial matrices in the delay operator
.
The disturbance model is taken as
with v a column vector of white noise inputs. The quantities
and 
are polynomial matrices in the delay operator, with
diagonal, and
for the plant. The polynomial matrix
follows by the spectral factorization
The superscript * denotes the adjoint, that is,
The spectral factor
needs to have all its roots
outside the unit circle.
The controller H may now be expressed as
where the polynomial matrix T, together with the polynomial matrix P, is the solution of the two-sided equation
reveals that
Furthermore, writing
we see that
The weighting matrices, finally, are selected as
% demoB
% Script for the demo "Control of a batch process"
% Define the data
L = [-77*z^-3 0.33*z^-3; 0 0.03*z^-3; 0 0.1*z^-3];
R = eye(2,2);
theta = diag([1-0.6*z^-1 1 1-0.55*z^-1]);
Phi = diag([1 1-0.5*z^-1 1]);
d = 1;
Q1 = diag([0.01 8 2.25]);
Nabla = (1-z^-1);
by spectral
factorization:
% Spectral factorization
Gamma = spf(L'*Q1*L);
The result is
Gamma
Constant polynomial matrix: 2-by-2
Gamma =
7.7 -0.033
0.00074 0.17
for the matrices T and P. For this we use the routine
axybc. This solves the two-sided polynomial matrix equation
To turn into a polynomial matrix equation we need to multiply it by a suitable power n of
so that 
and 
both are polynomial and also 
is a polynomial matrix.
Choosing n = 3 we have
% Solution of the two-sided
equation
n = 3;
A = z^-n*Gamma';
B = Nabla^d*Phi;
C = L'*Q1*theta;
[T,U] = axybc(A,B,C);
T turns out to be 2×3 matrix of degree 1, as predicted by the theory (MacGregor and Harris, 1987):
T =
-0.04 -0.00025 + 0.00012z^-1
-5.6e-005
-3.8e-006 2.6 - 1.2z^-1 0.59
where
is polynomial because
is a constant matrix. We compute the controller as
% Compute the controller H =
phi/theta
phi = R/Gamma*T;
The result is
phi =
-0.0052 0.065 - 0.03z^-1 0.015
-1.3e-016 15 - 7.1z^-1 3.4
The closed-loop response to the disturbances D(t) follows from the sensitivity matrix S:
It is not difficult to find from the block diagram of Fig. 1 that if the plant model exactly matches the plant then
It follows that
where
Thus we add the lines
% Compute the sensitivity
matrix S = psi/theta
psi = theta-L/Gamma*T;
% Plot the data
figure; clf
k = length(r);
for i = 1:k
for j = 1:k
subplot(k,k,(i-1)*k+j)
plot(0:n,r{:}(i,j))
grid on; axis([0 n -1.5 1.5])
end
end
Matlab produces the plot of Fig. 2 for the impulse response matrix. The step responses may be computed similarly and are shown in Fig. 3.
% Compute and plot the
disturbance step response matrix s
% Apply long division to (psi/theta)*1/(1-z^-1)
n = 10;
[q,s] = longrdiv(psi,theta*(1-z^-1),n);
% Plot
figure; clf
k = length(s);
for i = 1:k
for j = 1:k
subplot(k,k,(i-1)*k+j)
plot(0:n,s{:}(i,j))
grid on; axis([0 n -1.5 1.5])
end
end
Fig. 3. Disturbance step response matrix
Assesment
