Applications
in Behavioral Theory |
Signals, Systems and Control
Department
Faculty of Mathematical Sciences
University of Twente
The Netherlands
| To download the application in .pdf format, click here. |
Introduction |
Image Representation State Representation Example 3 IO System Construction Example 4 |
Polynomial matrices play an important role in the behavioral theory of linear systems. The purpose of this demo is to show that the Polynomial Toolbox provides many useful routines for dealing with problems and questions in behavioral linear system theory.
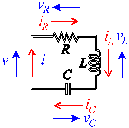 Fig. 1. RCL network
Example
Fig. 1. RCL network
Exampleresistor:
inductor:
capacitor:
![]()
![]()
All these equations can be combined in the form
![]()
where the polynomial matrix Q and the vector-valued signal z are given by
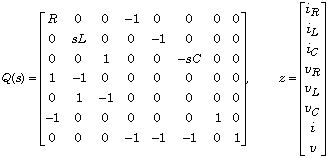
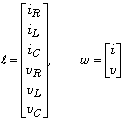
If the latent variables are eliminated from the behavior then the manifest behavior is obtained.
Compensation of the Manifest Behavior![]()
where s represents the differentiation operator. Let the rows of the polynomial matrix
![]()
where
![]()
![]()
We input the polynomial matrix Q as
Q = [ R 0 0 -1 0 0 0 0
0 s*L 0 0 -1 0 0 0
0 0 1 0 0 -s*C 0 0
1 -1 0 0 0 0 0 0
0 1 -1 0 0 0 0 0
-1 0 0 0 0 0 1 0
0 0 0 -1 -1 -1 0 1];
The polynomial matrices
From this, the matrices
R =
2 + 3s + s^2 -s
Hence, the manifest behavior is described by the differential equation
![]()
ans =
1
![]()
there always exists an equivalent images/demo_behav/Image representation of the form
![]()
with
M =
s
2 + 3s + s^2
Hence, the images/demo_behav/Image representation of the system is
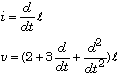
Note that physically the latent variable
![]()
The latent variable x is the state of the system. This representation is by no means unique, and may be constructed in the following way from the kernel representation
First, assume that R is row-reduced. If it is not then it may be unimodularly transformed to be row-reduced without changing the behavior.
Let S be a square, nonsingular, row-reduced matrix whose row degrees equal the row degrees of R, and chosen such that
![]()
Let
![]()
be a minimal realization of the left coprime matrix fraction
![]()
is a state realization of the behavior.
ExampleR =
2 + 3s + s^2 -s
we choose
A minimal realization of
A =
0 1
0 0
B =
3.0000 -1.0000
2.0000 0
C =
1 0
D =
1 0
If no compelling reason exists to designate certain manifest variables as inputs and other variables as outputs then possible partitionings of the manifest variables into sets of input variables and output variables may be determined on the basis of the (plausible) requirement that the outputs are causally affected by the inputs.
To make this more concrete, suppose that we have a kernel representation
![]()
with y the output and u the input. Then the proposed selection of outputs and inputs is deemed acceptable if
Consider the state representation
![]()
where C and D have r rows. Then in this context a causal IO representation may be constructed by selecting r columns of D so that the resulting square submatrix is nonsingular. By designating the corresponding entries of w as outputs and the remaining entries as inputs the equation
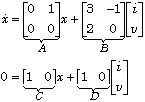
Inspection of the matrix D shows that the only available option is to take the current i as the output and, hence, the voltage as the input. Substitution of the resulting output
![]()
into the first equation yields the corresponding state differential equation. Not wanting to make any mistakes we invoke Matlab:
a =
-3.0000 1.0000
-2.0000 0
b =
-1.0000
0
Thus, we have the IO representation
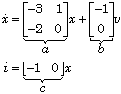
This selection of input and output corresponds to connecting the network to a voltage source. Connecting it to a current source does not lead to a causal IO system because the admittance
![]()
of the network is nonproper.