Recommended Publications on Polynomial Methods

Return to the tutorials

Books with major contributions on polynomial matrices

Barnett S. (1983), Polynomial and Linear Control Systems, Pure and Applied Mathematics, Marcel Dekker.

Callier F. M. and C. A. Desoer (1982), Multivariable Feedback Systems, Springer-Verlag, New York.

Chen Ch. (1984), Linear System Theory and Design, Holt, Rinehart and Winston, New York.

Gohberg I., P. Lancaster and I. Rodman (1982), Matrix Polynomials, Academic Press, New York.

Kailath T. (1980), Linear Systems, Prentice Hall, Englewood Cliffs, N.J.

Kucera V. (1979), Discrete Linear Control, New York: Wiley.

Stefanidis P., A. P. Paplinski and M. J. Gibbard (1992), Numerical Operations with Polynomial Matrices : Application to Multi-Variable Dynamic Compensator Design. Lecture Notes in Control and Information Sciences, Vol. 171, Springer-Verlag, 1992.

Wolovich W. A. (1974)}, Linear Multivariable Systems, Springer, New York.

Other books with material on polynomial matrix methods

Dorf, R. C. (1989), Modern Control Systems, 5th Ed. Addison-Wesley.

Gantmacher F. R. (1960), The Theory of Matrices, Chelsea Publishing Company, New York.

Kucera, V. (1991), Analysis and Design of Discrete Linear Control Systems, Academia and Prentice Hall, Prague and London.

Rosenbrock H. H. (1970), State space and multivariable theory. Wiley-Interscience, New York.

Applications to signal processing

T. Söderström, J. Jezek and V. Kucera (1997), "An efficient and versatile algorithm for computing the covariance function of an ARMA process." Accepted for publication in IEEE Trans. Signal Processing.

H-infinity optimization

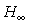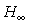Kwakernaak H. (1991), "The polynomial approach to -optimal regulation", in E. Mosca and L. Pandolfi, Eds., Control Theory, Lecture Notes in Mathematics 1496, Springer-Verlag, Berlin.

Kwakernaak H. (1993b), "Robust control and 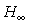optimization," Automatica, 29, pp. 255-273.

Kwakernaak H. (1996), "Frequency domain solution of the standard 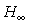problem." In M. J. Grimble and V. Kucera, Eds., Polynomial Methods for Control Systems Design, Springer-Verlag.

Interpolation methods

Antsaklis P. J. and Z. Gao (1992), "Polynomial and rational matrix interpolation: Theory and control application." Control Systems Technical Report No. 71, University of Notre Dame, Indiana, U.S.A.

Linear polynomial matrix equations

Kucera V. (1993), "Diophantine equations in control - a survey", Automatica 29, 6, pp. 1361-1375.

Numerical methods related to polynomial matrices

Golub G. H. and C. F. Van Loan (1989), Matrix Computations, John Hopkins University Press, second edition.

Polynomial matrix fractions

Datta K. B. and S. Gangopadhyay (1992), "Coprime matrix fraction description via orthogonal structure theorem," IEEE Trans. Aut. Control, 37, pp. 1517-1520.

Patel R. V. (1981), "Computation of matrix fraction descriptions of linear time-invariant systems," IEEE Trans. Aut. Control, 26, pp. 148-161.

Strijbos R. C. W. (1995a). "Calculation of right matrix fraction descriptions; an algorithm," Memorandum No. 1287, Faculty of Applied Mathematics, University of Twente.

Strijbos R. W. C. (1996), "Calculation of right matrix fraction descriptions; an algorithm,'' Proceedings of the 4th IEEE Mediterranean Symposium on New Directions in Control and Automation, Maleme, Krete, Greece, June 10-13, pp. 478-482.

Polynomial matrix algorithms

Henrion D. and M. Sebek (1996), "Symmetric matrix polynomial equations." Submitted.

Henrion D. and M. Sebek (1997), "An efficient numerical algorithm for the discrete time symmetric matrix polynomial equation." Proc. 1997 European Control Conference, Brussels.

Kraffer, F., M. Sebek and S. Pejchová (1994), "Numerical performance in matrix Diophantine equation", Kybernetika 30, 6, pp. 745-753.

Kwakernaak H. (1993a), "State space algorithms for polynomial matrix computations," Memorandum No. 1168, Faculty of Applied Mathematics, University of Twente.

Sebek M., S. Pejchová and F. Kraffer (1994), "Testing algorithms for linear polynomial equations", Proceedings of the 33rd IEEE Conference on Decision and Control, IEEE Control Systems Society, pp. 2518-2519, Orlando, Fl.

Sebek M., F. Kraus, S. Pejchová, H. Kwakernaak and D. Henrion (1996), "Numerical methods for zeros and determinant of polynomial matrix." Proc. 4th IEEE Mediterranean Symposium on Control and Automation, Chania, Crete, Greece, June 1996.

Sebek, M., D. Henrion, S. Pejchová and H. Kwakernaak (1997), "Numerical methods for zeros and determinant of polynomial matrix", Kybernetika (to appear).

Sebek M. and P. Husek (1997), "Basic routines for rational matrices: a critical comparison", Proceedings of the 5th IEEE Mediterranean Symposium on New Directions in Control and Automation, Paphos, Cyprus.

Software

Kwakernaak H. (1990), "MATLAB macros for polynomial 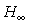control system optimization," Memorandum No. 881, Faculty of Applied Mathematics, University of Twente.

Strijbos R. C. W. (1995b), "A polynomial toolbox; implementation aspects," Memorandum No. 1288, Faculty of Applied Mathematics, University of Twente.

Spectral factorization

Callier F. M. (1985), "On polynomial matrix spectral factorization by symmetric factor extraction", IEEE Trans. Aut. Control 30, pp. 453-464.

Jakubovic V. A. (1970), "Factorization of symmetric matrix polynomials", Dokl. Acad. Nauk. SSSR, 194, 3, pp. 1261-1264.

Jezek J. and V. Kucera (1985), "Efficient Algorithm for Matrix Spectral Factorization'', Automatica, Vol. 21, No. 6, pp 663-669.

Kwakernaak H. and M. Sebek (1994), "Polynomial J-Spectral Factorization'', IEEE Transactions on Automatic Control, Vol. 39, No. 2, pp 315-328.

Sebek, M. (1993), "J-Spectral factorisation algorithms", in ed. K. J. Hunt, Polynomial Methods in Optimal Control and Filtering, Ch. 10, pp. 278-307. Peter Peregrinus, Ltd, London.